This text will delve into what precisely put/name parity is, the precise components for calculating it, and the way changing into accustomed to this idea can deepen your understanding of the choices market.
What’s Put/Name Parity?
Put/name parity is an idea that defines the mathematical relationship between the costs of put choices and name choices which have the identical strike worth and expiration date. In different phrases, if a name possibility is buying and selling at X, the put possibility of the identical strike and expiration date must be buying and selling at Y, and vice versa.
Put merely, put/name parity realizes that you should utilize totally different combos of choices to create the identical place and formalizes this mathematical relationship between places and calls.
For example, combining shares of the underlying with an at-the-money put is nearly equivalent to purchasing an at-the-money name. Put/name parity assumes these two equivalent portfolios ought to value the identical.
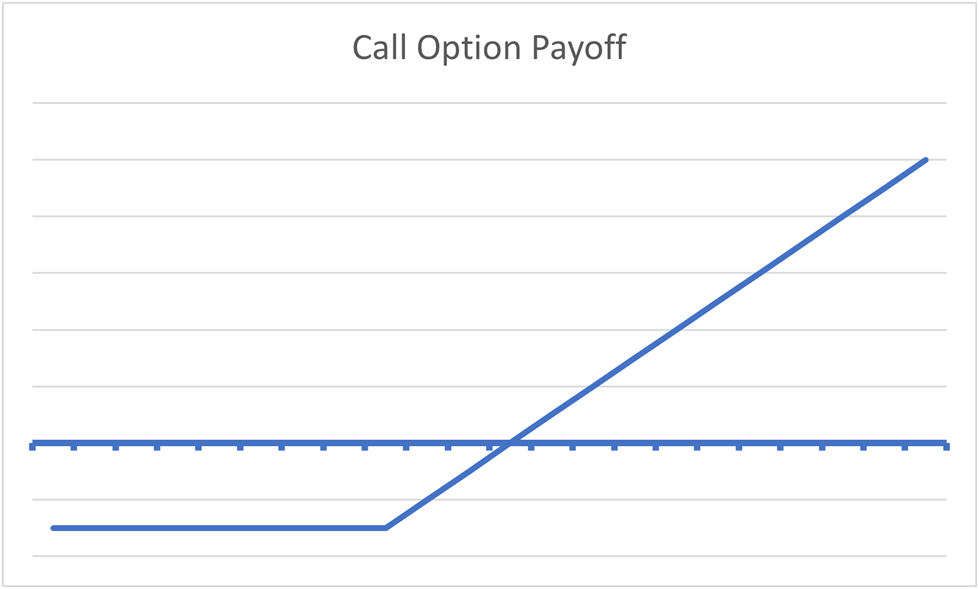
To offer you a visible, each our “artificial name” place and shopping for a name possibility outright have an equivalent payoff, as you may see within the payoff diagram beneath:
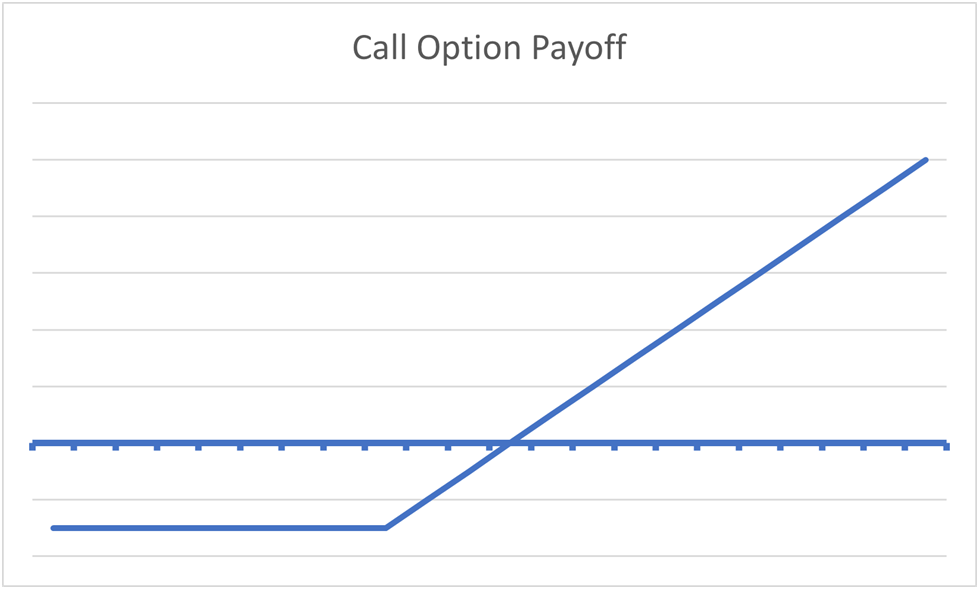
Put/name parity formalizes the arithmetic behind places and calls and provides every possibility a definitive intrinsic worth. The introduction of synthetics means that there is a direct arbitrage element to choices, making certain that opportunistic merchants at all times preserve the costs of choices in line.
For example, a risk-free arbitrage alternative exists if an artificial name possibility might be bought cheaper than the decision possibility outright, incentivizing merchants to push costs again to their honest values.
Put/Name Parity Formulation
Put/name parity has an easy components that basically means that you can worth out the honest worth of a put possibility relative to its equal (identical strike worth and expiration date) name possibility and vice versa.
Put/name parity solely applies to choices with the identical strike worth and expiration date. For instance, utilizing this components, you may evaluate the $101 strike put and name that each expire in 21 days, however you can’t evaluate the $101 strike put and $103 strike name with totally different expirations.
The put/name parity is as follows:
C + PV(x) = P + S
The place:
● C = the worth of the decision possibility
● P = the worth of the put possibility
● PV (x) = the current worth of the strike worth
● S = present worth of the underlying asset
So let’s plug in some precise numbers into the components and stroll by way of it. We’ll begin with the worth of the underlying.
Let’s assume the underlying is buying and selling at $61.66, and we’re wanting on the $70 strike name possibility, which is buying and selling for $1.45 and expires in 25 days.
So let’s revise our components by plugging in $1.45 for C, which is the worth of the decision possibility, and $61.66 for S, which is the worth of the underlying.
$1.45 + PV(x) = P + 61.66
Now we now have two values left to find out. PV(x) refers back to the current worth of the strike worth. However what does that imply? As a result of an possibility is an settlement to purchase or promote at a specified worth at a date sooner or later, we now have to low cost the strike worth to the current to account for the time worth of cash. We use the risk-free rate of interest (mostly the annualized price of a 3-month US treasury invoice) to low cost the strike worth to the current. On the time of writing, that price is at 4.7%, so the maths would appear like this:
PV(x) = S / (1 + r)^T
The place:
● S = the strike worth of the underlying
● R = the risk-free rate of interest in decimals
● T = time to expiration in years, in decimals
To show our time-to-expiration right into a decimal, we merely divide our time-to-expiration by 365 as in 25/365 = 0.068
So our components would appear like this:
PV(x) = $70 / (1 / 0.047)^0.068 = $69.79
So this brings the current worth of the strike worth to $4076.16. So let’s plug within the final worth to our components:
$1.45 + 69.79 = P + 61.66
So to unravel for P, or the worth of the same-strike, same-expiration put possibility, we sum our name possibility worth and the current worth of our strike, which brings us to 71.24. Then we subtract the spot worth of the underlying from 71.24, which is 9.58.
Being formulated within the Nineteen Sixties, the put/name parity components has some crucial limitations within the fashionable period.
Put/Name Parity Applies to European Choices
The unique put/name parity components launched by Hans Stoll in 1969 applies particularly to European choices. When introducing American-style choices, the maths adjustments a bit as a result of you may train them anytime till expiration.
If you could get extra accustomed to the distinction, learn our article on Choices Settlement, which matches into the variations between European and American-style choices.
However briefly, European choices are cash-settled and might solely be exercised at expiration. American choices are bodily settled, which suggests settlement includes the precise switch of the underlying asset, and they are often exercised at any time till expiration.
Index and futures choices are European-style, whereas inventory choices are American-style choices.
There may be nonetheless a put/name parity relationship in American choices. The mathematics is only a bit totally different. See these NYU lecture notes to see a breakdown of the maths.
Put/Name Parity Doesn’t Account for Dividends or Curiosity Funds
The following level is that the put/name parity components would not contemplate any money flows accrued by holding the underlying asset, like curiosity funds or dividends. These additionally alter the calculation.
Should you have been to plug in a bond or dividend-paying inventory into the put/name parity components, you’d discover that the numbers would not add up. That is as a result of the components would not account for the current worth of money flows like dividends or curiosity funds. You can too adapt the components to work with money flows, however that is past the scope of this text.
Put/Name Parity Doesn’t Account For Transaction Prices or Charges
And eventually, the put/name parity doesn’t take any transaction prices, taxes, commissions, or some other extraneous prices under consideration.
Artificial Replication
Within the introduction to this text, we talked about how you should utilize totally different combos of choices to create two portfolios with equivalent payoffs. We talked about how combining a put possibility and the underlying inventory provides you a similar payoff as shopping for a name possibility.
This concept is named artificial replication. You could possibly create a place with an equivalent payoff and threat profile, albeit with a special mixture of securities. Getting a tough understanding of synthetics provides choices merchants a greater grasp of the true nature of choices and the way they are often infinitely mixed to change your market view.
Utilizing the constructing blocks of quick/lengthy places or calls and quick/lengthy the underlying asset, you may replicate practically any choices place. Listed here are the fundamental examples:
● Artificial Lengthy Underlying: quick put + lengthy name
● Artificial Quick Underlying: quick name + lengthy put
● Artificial Lengthy name: lengthy underlying + lengthy put
● Artificial Quick Name: quick underlying + quick put
● Artificial Lengthy Put: quick underlying + lengthy name
● Artificial Quick Put: lengthy underlying + quick name
From right here, we are able to focus on conversions, reversals, and field spreads, that are all arbitrage methods merchants use to use possibility costs once they deviate from put/name parity. Keep in mind that your common dealer won’t ever make these trades, however studying how they work provides you a deeper appreciation of the choices market.
Put/Name Parity: The Beginnings of Choices Math
To offer you a bit of background, again within the Nineteen Sixties, the choices market was very small. Even essentially the most astute merchants did not know the way to worth choices, and it was a wild west. Hans R. Stoll was one of many few lecturers to essentially dig into the weeds of choices pricing in his seminal paper The Relationship Between Put and Name Choice Costs printed in 1969.
His work predated the work of Black, Scholes, and Merton’s groundbreaking Black-Scholes mannequin in 1973.
Stoll discovered that generally these artificial positions might be bought for cheaper than the precise positions. For example, if the market was very bullish on a inventory and merchants have been shopping for calls, you may purchase the underlying with an at-the-money and create an artificial name possibility for cheaper than shopping for an at-the-money name possibility. Basically, an arbitrage existed inside the choices market that would not exist inside an environment friendly market.
The Precept of No-Arbitrage
Put/name parity is a elementary idea in choices pricing, which assumes that two portfolios with equivalent payoffs ought to have the identical worth.
That is an extension of probably the most crucial ideas in monetary idea: the precept of no arbitrage. Put merely, it is the idea that you would be able to’t make risk-free earnings by exploiting market inefficiencies.
To narrate issues on to put/name parity, beneath the regulation of no-arbitrage, you need to by no means be capable of replicate the payoff of one other portfolio and purchase it for cheaper. For example, an artificial inventory ought to value the identical as shopping for the underlying inventory.
All spinoff pricing fashions use the precept of no arbitrage as a built-in assumption, permitting the mannequin to make estimates primarily based on the financial actuality that merchants will exploit and shut any pure arbitrage alternatives as they come up.
Backside Line
Put/name parity is a elementary idea that every one intermediate choices merchants ought to grow to be accustomed to. It is often the case that any name/put might be reconstructed utilizing another inventory plus put/name (respectively) mixture. Understanding put/name parity won’t ever make a dealer cash, however studying these ideas is a part of growing a broader consciousness of how the choices market works.
Associated articles
Subscribe to SteadyOptions now and expertise the total energy of choices buying and selling at your fingertips. Click on the button beneath to get began!